การคำนวณทางด้านกลศาสตร์โครงสร้าง (STRUCTURAL MECHANICS COMPUTATION หรือ SMC)
หัวข้อในวันนี้จะเกี่ยวข้องกันกับหัวข้อ การคำนวณทางด้านกลศาสตร์โครงสร้าง (STRUCTURAL MECHANICS COMPUTATION หรือ SMC) นะครับ
เนื่องจากเมื่อหลายวันก่อนหน้านี้ผมได้โพสต์ให้เพื่อนๆ ได้ทราบ และ มีความรู้ในเรื่อง เส้นอิทธิพล หรือว่า INFLUENCE LINE และ จากนั้นก็มีคำถามมาจากน้องวิศวกรท่านหนึ่งมาว่า
“เคยได้ยินถึงชื่อทฤษฎี MULLER-BRESLAU PRINCIPLE จึงมีความสนใจ และ อยากรบกวนขอให้ผมช่วยทำการอธิบายและขยายความให้หน่อยนะครับ”
ด้วยความยินดีเลยครับ เพราะ หากเมื่อเพื่อนๆ ได้อ่านบทความของผมแล้วเกิดข้อสงสัยประการใดก็ตามแต่ ผมก็แค่คาดหวังและอยากให้มีการซักถามเข้ามาแบบนี้แหละครับ
ทฤษฎี MULLER-BRESLAU PRINCIPLE คือ หลักการง่ายๆ ที่เราสามารถนำมาประยุกต์ใช้เพื่อทำการสร้าง เส้นอิทธิพล หรือว่า INFLUENCE LINE สำหรับโครงสร้างทั้งในรูปแบบ STATICALLY DETERMINATE STRUCTURES และรูปแบบ STATICALLY INDETERMINATE STRUCTURES เลยนะครับ
ซึ่งหลักการง่ายๆ ที่ว่านี้ คือ หากเราต้องการที่จะสร้าง เส้นอิทธิพล ณ ตำแหน่งใด หรือ แรงกระทำในรูปแบบใด ก็ตามแต่ แค่เพียงเราทำการแทนจุดหมุนภายใน (INTERNAL HINGED) ลงไป ณ ตำแหน่งนั้น และ ทำการสังเกตดูว่าโครงสร้างนั้น จะมีรูปแบบการเสียรูปอย่างไร ดังนั้นรูปร่างของ เส้นอิทธิพล ที่เราต้องการจะทราบก็คือรูปแบบของการเสียรูปของโครงสร้างอันเนื่องมาจากการแทนด้วยจุดหมุนภายในนี้นั่นเองนะครับ
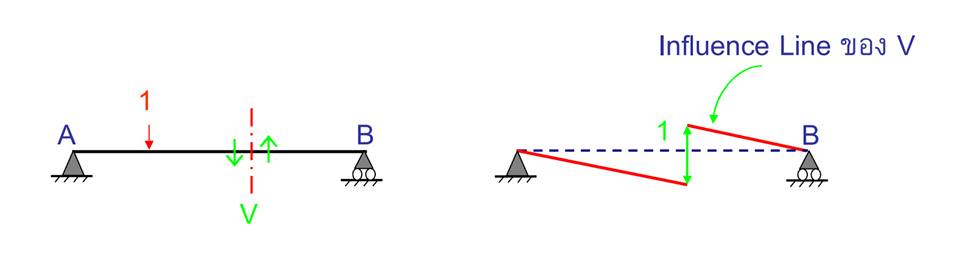
ตัวอย่าง ที่ผมนำมาฝากเพื่อนๆ ทุกคนในวันนี้คือ ในกรณีที่เราต้องการที่จะสร้าง เส้นอิทธิพล ของค่าแรงเฉือน (SHEAR FORCE) ณ ช่วงหนึ่งของคานนะครับ
โดยลำดับขั้นตอนในการประยุกต์ใช้ทฤษฎี MULLER-BRESLAU PRINCIPLE คือ ให้เราเริ่มต้นจากการแทนให้
ณ ตำแหน่งนั้น มี จุดหมุนภายใน แทนที่ลงไปในโครงสร้างคาน จากนั้นก็ทำให้ ณ ตำแหน่งนั้น เกิดการเคลื่อนที่สัมพัทธ์มีค่าเท่ากับ 1 หน่วย แค่เพียงเท่านี้เราก็จะมองเห็นได้ว่าเส้นแนวการเสียรูป (DEFLECTED SHAPE) ในโครงสร้างนั้นเป็นไปในรูปแบบใด ซึ่งเส้นแนวการเสียรูปที่เกิดขึ้นนี้ก็คือ เส้นอิทธิพล ของโครงสร้างที่เราต้องการนั่นเองนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ